Progress Studies in Mathematics

A new series on a fundamental progress prerequisite

The fruits of technological progress are impossible to ignore. Almost all of the buildings, vehicles, and tools that we interact with could not have been built even a hundred years ago. What is easier to miss is the common roots that all of these advances share in our knowledge of mathematics.

Mathematics is essential to particle physics, agriculture, digital computing, air transportation, plumbing, and much more. Each of these pursuits relies explicitly on a mathematical model, and often one that was developed within the last century. Progress in mathematics is necessary, though not sufficient, for scientific and technological progress in general. Despite this importance, mathematics is understudied in the progress studies community.

This post will be the first in a series chronicling the development of math throughout human history in an attempt to discover general principles underlying the progress in this fundamental field. In this introductory post I will consider different ways we might measure progress in math and give an overview of the scale and importance of mathematical progress to this point.

How Should Progress In Math Be Measured?

Answering this question rigorously would first require a definition for what progress means in this context. Without committing to one, however, we can take a pluralist approach and see if there are common trends among many different measurements.

Inputs

One measure of progress in the field is the number of people who research mathematics. All sources on this question are incomplete, especially when considering mathematicians outside of the US, but it is clear that the population of math researchers has increased significantly over the past 50 years at least. According to the Mathematics Genealogy Project, this is the number of new math PhDs awarded each year since 1961.

More researchers means more ideas and faster progress. There may also be increasing returns to scale as the idea-sharing network of each existing researcher gets larger with every new addition, and high fixed cost investments into research facilities can be amortized among more users.

Outputs

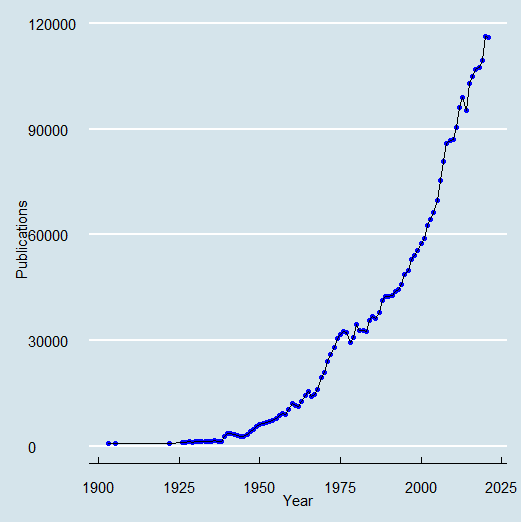
The main product of these PhDs, academic papers, has also been prodigiously growing over the past century. As tracked by the American Mathematical Society, there are now over a hundred thousand new papers published in mathematics each year.

These charts show massive increases in the inputs and outputs in the field of mathematics, but they may overstate the case for progress if the impact of each individual researcher or publication is decreasing. This seems possible as the modal math paper in the ancient world might have been an important low-hanging-fruit result in geometry or number theory, while the modal paper today is probably something about Frobenius Betti numbers and syzygies of finite length modules. There is definitely a selection effect for which ancient theorems are passed down to the present, but more than 75 of mathematician Paul Abad’s list of the 100 greatest theorems came before 1900 despite the many millions more math papers published after that date than before it.

We might also look at lists of unsolved problems or developments assembled by experts and evaluate the field’s performance in solving them. Of David Hilbert’s list of 23 problems posed at the beginning of the 20th century, over half have been solved or at least partially solved today. Of seven problems in the list of Millennium Problems posed in the year 2000, one has been solved so far. In his article “Has Progress In Mathematics Slowed Down?”, mathematician Paul Halmos considers a list of problems unsolved or unknown to 19th century mathematician Richard Dedekind. His list contains 22 elements and it is made up of individual proofs, entire fields, or just ideas, including The Monte Carlo Method, Fast Fourier Transforms, The Four Color Theorem, and Catastrophe Theory. The article ends with the claim that “The answer to the question in the title is clearly and decisively no.”

Capabilities

The preceding measurements all considered the progress of mathematics at the frontier, but the use of mathematics by non-specialists may be its most important source of impact. 500 years ago only the most educated would know any algebra or geometry and no calculus at all. 200 years later not much had changed, although a handful of preeminent mathematicians understood the beginnings of calculus. 50 years ago fewer than 2% of high school students took AP calculus, now over 10% do.

As concepts trickle down from the greatest mathematicians on earth to above average high school students, the impact of any one mathematical idea is multiplied across all the people who use it, perhaps with increasing returns to scale as disparate concepts and fields are linked by shared mathematical models. Advances in theoretical and statistical modelling are increasing the standard of knowledge in numerous academic disciplines outside of mathematics, including physics, economics, and epidemiology. Thanks to the information revolution, this dissemination of mathematical knowledge has never been easier. There are thousands of free videos, courses, and practice problems which are probably the best pieces of mathematics education ever created thanks to never-before-possible use of animations alongside explanations.

The most optimistic view of progress in mathematics comes from examining our capacity for computation over time.

Knowing a trillion more digits of pi isn’t that important; the hundred digits we knew in 1750 are more than enough for our most precise calculations in the physical world, but maintaining such a steep growth curve on a logarithmic scale is indicative of the incredibly powerful underlying trend of increasing computing power.

Somewhat unscientific charts like this, which show the correlation between growth in computing power and growth in the global economy, are believably causal when one considers the pervasiveness of digital technology. Increases in computing ability have of course ushered in a golden age of consumer technology, but they have also facilitated new uses for theoretical models which were once far too computationally expensive to be practically useful. These include density functional theory which, when paired with huge compute power, allows extremely accurate simulations of quantum mechanical chemistry, gigantic neural networks becoming much more competent when combined with big data, and genome sequencing becoming 100,000% cheaper within 15 years.

We are still left without a unified measure of progress in mathematics, but our pluralistic exploration has confirmed that math has come far and is growing faster than ever. This is a good thing too because looking into the future, it seems likely that mathematics will retain its position at the foundation of our most important technological advancements. Cryptography, space travel, machine learning, genomics, and quantum computing are fundamentally math problems, and they are all advancing thanks to the application of new models and newfound computing power.

We should not rest on our laurels, however. Stagnation and regress in mathematics has happened before. Math’s importance to future progress, and the variability of its growth over time tells us that it is both possible and desirable to accelerate progress in mathematics.

Pursuing understanding of the history of mathematics and the acceleration of its future, in the next posts I will research math’s impacts on the Neolithic, urban, and Industrial revolutions, how math education and research has changed over time, and how it might be better organized in the future. Subscribe to read future posts on Progress Studies in Mathematics.

---